viernes, 15 de octubre de 2010

Movimiento Periódico

Definición

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación
x=A·sen(ωt+φ)

donde

A es la amplitud.

w la frecuencia angular.

w t+j la fase.

j la fase inicial.

Las características de un M.A.S. son:

Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre -A y +A.

La función seno es periódica y se repite cada 2p, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2p, es decir, cuando transcurre un tiempo P tal que w(t+P)+j=w t+j+2p .

P=2π/ω

Cinemática de un M.A.S.

En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad.
La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación
x=A·sen(ωt+φ)
Derivando con respecto al tiempo, obtenemos la velocidad del móvil

Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil

Este resultado se suele expresar en forma de ecuación diferencial

Esta es la ecuación diferencial de un MAS donde x puede ser cualquier magnitud: un desplazamiento lineal, un desplazamiento angular, la carga de un condensador, una temperatura, etc.
Puede comprobarse que la solución de esta ecuación diferencial es
x=A sen(w t+j )
Condiciones iniciales
Conociendo la posición inicial x₀ y la velocidad inicial v₀ en el instante t=0.
x₀=A·senj
v₀=Aw·cosj
se determinan la amplitud A y la fase inicial φ

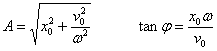
Dinámica de un M.A.S.

Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.

Como la fuerza F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial E_p.

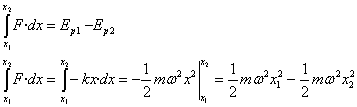
La expresión de la energía potencial es

Donde c es cualquier constante. Se toma como nivel cero de la energía potencial E_p=0 cuando el móvil está en el origen, x=0, por lo que c=0
La energía total E, es la suma de la energía cinética E_k y de la energía potencial E_p que es constante.

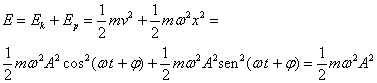
MAS y movimiento circular

La ecuación de un M.A.S. es
x=A·sen(ωt+φ)

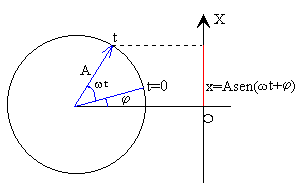En la figura, se observa la interpretación de un M.A.S. como proyección sobre el eje X, del extremo de un vector rotatorio de longitud igual a la amplitud A, que gira con velocidad angular w igual a la frecuencia angular del M.A.S, en el sentido contrario a las agujas del reloj.

El ángulo w t+j que forma el vector rotatorio con el eje de las X se denomina fase del movimiento. El ángulo j que forma en el instante t=0, se denomina fase inicial.

Energía en el Movimiento Armónico Simple

La energía cinética de una partícula es Ec = 1/2 mv² = 1/2 mw²A²cos²(wt +f₀), o en función del desplazamiento

E_c = 1/2 mw²(A²- x²)

Energía potencial

Recordando que F = -dEp/dx y que F = -Kx se obtiene que dEp/dx = Kx

Integrando y eligiendo el cero de la energía potencial en la posición de equilibrio (x=0):

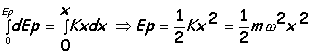
La energía potencial es mínima en la posición de equilibrio y máxima en los extremos x=±A

Sumando la energía cinética y potencial se obtiene la siguiente expresión:

E =Ec +Ep = 1/2 mw²(A²- x²) + 1/2 mw² x² = 1/2 mw²A²= 1/2Kx²

Durante la oscilación, como muestra el diagrama, hay un intercambio de energía cinética y potencial, manteniéndose la energía total constante ya que se trata de una fuerza conservativa. La figura muestra una energía total de 15 unidades correspondientes a la línea horizontal negra. La línea vertical roja muestra la diferencia entre la energía total y la potencial (indicada por la línea discontinua sobre el eje de abcisas) y por tanto corresponde a la energía cinética. Los límites de oscilación están determinados por sus intersecciones con la curva de energía potencial y corresponden a los puntos ±A.

Dinámica del Movimiento Rotaciónal

Péndulo de torsión

El péndulo de torsión es un ejemplo de movimiento armónico simple, consiste en un disco o cilindro sólido sostenido por una barra delgada. Si se hace girar el disco en la medida de un ángulo . El momento de torsión es directamente proporcional al desplazamiento angular. Se tiene:

donde k’ es una constante que depende del material de que esta hecha la barra delgada. El periodo del movimiento armónico simple angular esta dado por:

donde I es el momento de inercia del sistema de vibración

*Péndulo* *Simple* Llamamos péndulo simple a un ente ideal constituido por una masa puntual suspendido de un hilo inextensible y sin peso, capaz de oscilar libremente en el vacío y sin rozamiento. Al separar la masa de su posición de equilibrio, oscila a ambos lados de dicha posición, realizando un movimiento armínico simple. En la posición de uno de los extremos se produce un equilibrio de fuerzas, según observamos en el gráfico:

	El peso de la bola se descompone en dos componentes: una primera componente que se equilibra con la tensión del hilo, de manera que: La segunda componente, perpendicular a la anterior, es la que origina el movimiento oscilante: Sin embargo, para oscilaciones de valores de ángulos pequeños, se cumple: .
Comprobamos en la tabla siguiente, con datos de ángulos y sus senos, esta afirmación. Por consiguiente, podremos escribir, teniendo en cuenta, el valor del seno del ángulo: Se observa que la fuerza recuperadora, que hace oscilar al péndulo, es función de la elongación (X), con lo que podemos afirmar que se trata de un M. A. S. Por ello, podemos comparar la ecuación que caracteriza a este tipo de movimientos, que vemos a continuación: ,con la ecuación obtenida anteriormente vemos que la pulsación es:,y teniendo en cuenta que donde T es el período: Tiempo utilizado en realizar una oscilación completa, llegamos a: A continuación, tienes un péndulo. Haz click en la masa y coloca distintas longitudes. Observarás como cambia el período, de forma que al aumentar la longitud, aumenta T. El péndulo físico Un cuerpo rígido que gira libremente en torno a un eje fijo de rotación, que no coincide con su centro de gravedad, constituye un péndulo físico. Las leyes de la dinámica de rotación establecen que el momento de las fuerzas que actúan sobre el cuerpo es igual al momento de inercia del cuerpo multiplicado por la aceleración angular a que es sometido: (1) Donde M es el momento de las fuerzas que actúan sobre el sistema, I el momento de inercia del cuerpo respecto del eje de oscilación (O) y el ángulo que nos da la posición del cuerpo respecto de la de equilibrio. Por tanto la derivada segunda de respecto del tiempo dos veces es la aceleración angular del sistema. Figura 1 - El péndulo físico El momento de la fuerza de la gravedad que actúa sobre un péndulo físico como el de la figura 1, cuando el sistema forma un cierto ángulo respecto a la posición de equilibrio, se puede expresar, en función de ese ángulo como: (2) Donde m es la masa del péndulo, a es la distancia del eje de oscilación O al centro de gravedad y el signo indica que es un momento recuperador, que tiende a llevar al sistema a la posición de equilibrio. Hemos empleado la aproximación del seno de un ángulo por el propio ángulo, válido para oscilaciones pequeñas, de forma que al realizar la experiencia tendremos que cuidarnos de que esta hipótesis se cumpla, es decir hacer oscilar al péndulo con un ángulo pequeño. Igualando las dos expresiones anteriores (1) y (2), obtenemos la que nos da el periodo del péndulo físico: (3) Para la posterior comparación con los valores experimentales podemos poner, en esta expresión, el momento de inercia respecto al eje de oscilación en función del momento de inercia respecto del centro de masas, a través del teorema de Steiner, en el que el momento del centro de gravedad será la suma del momento de la barra y el de las dos masas con las cuchillas: Y sustituyendo en la expresión (3), obtenemos: (4) En el caso del péndulo simple o péndulo matemático esta expresión se simplifica en la siguiente: (5) Donde es la distancia del eje de giro al centro de gravedad que en el péndulo matemático es la longitud del péndulo. Por tanto, si igualamos las dos expresiones (3) y (5) obtenemos: (6) Que nos da la de un péndulo matemático del mismo periodo de oscilación que el péndulo físico que estamos estudiando. A este valor se le llama longitud reducida del péndulo físico.

Rotación de Cuerpos Rígidos

Movimiento circular uniforme

Un movimiento circular uniforme es aquél cuya velocidad angular w es constante, por tanto, la aceleración angular es cero. La posición angular q del móvil en el instante t lo podemos calcular integrandoq -q₀=w(t-t₀)o gráficamente, en la representación de w en función de t.

Habitualmente, el instante inicial t₀ se toma como cero. Las ecuaciones del movimiento circular uniforme son análogas a las del movimiento rectilíneo uniforme

Movimiento circular uniformemente acelerado

	Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante.Dada la aceleración angular podemos obtener el cambio de velocidad angular w -w₀ entre los instantes t₀ y t, mediante integración, o gráficamente.
	Dada la velocidad angular w en función del tiempo, obtenemos el desplazamiento q -q₀ del móvil entre los instantes t₀ y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

Habitualmente, el instante inicial t₀ se toma como cero. Las fórmulas del movimiento circular uniformemente acelerado son análogas a las del movimiento rectilíneo uniformemente acelerado.

Despejando el tiempo t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ₀

Velocidad angular y velocidad tangencial

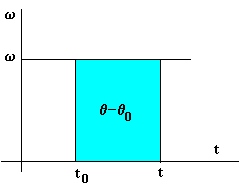
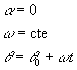
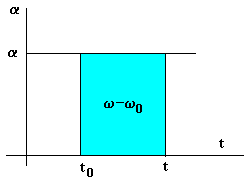
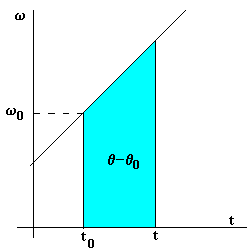
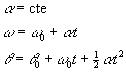
Velocidad angular es la variación del arco respecto al tiempo, se lo señala con la letra $\omega \,$ , se define como:

$\omega = \frac{d \varphi}{d t}$

Velocidad tangencial de la partícula es la velocidad real del objeto que efectúa el movimiento circular, puede calcularse a partir de la velocidad angular. Si v_tes la velocidad tangencial, a lo largo de la circunferencia de radio R, se tiene que:

$v_t = R\omega\,$ .

Aceleración angular

Se define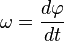 la aceleración angular como la variación de la velocidad angular por unidad de tiempo y se la representa con la letra: $\alpha\,$ y se la calcula: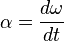

$\alpha = \frac{d \omega }{d t}$

Si a_t es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:

$a_t = R \, \alpha \;$

Período y frecuencia

El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Su fórmula principal es:

$T=\frac{2\pi}{\omega}$

La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo, usualmente segundos. Se mide en hercios o s^-1

$f=\frac{1}{T}=\frac{\omega}{2\pi}$

Aceleración y fuerza centrípetas

La aceleración centrípeta o aceleración normal afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. La fórmula para hallarla es:

$a_c = a_n = \frac{v^2_t}{R}=\omega^2R$

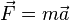La fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la masa del móvil, y basándose en la segunda ley de Newton ( $\vec {F} = m \vec {a}$ ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula: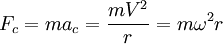

$F_c=ma_c=\frac{mV^2}{r}=m\omega^2r$

Definición de momento de inercia

El momento de inercia o inercia rotacional es una magnitud que da cuenta de cómo es la distribución de masas de un cuerpo o un sistema de partículas alrededor de uno de sus puntos. Este concepto, desempeña en el movimiento de rotación un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme.

Dado un eje arbitrario, para un sistema de partículas se define como la suma de los productos entre las masas de las partículas que componen un sistema, y el cuadrado de la distancia r de cada partícula a al eje escogido. Representa la inercia de un cuerpo a rotar. Matemáticamente se expresa como:

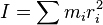
$I = \sum m_ir_i^2 \,$

Para un cuerpo de masa continua (Medio continuo) lo anterior se generaliza como:

$I = \int_V r^2 dm = \int_V \rho r^2 \,dV$

El subíndice V de la integral indica que hay que integrar sobre todo el volumen del cuerpo.

Este concepto, desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. Así, por ejemplo, la segunda ley de Newton: $\scriptstyle{F = ma}$ tiene como equivalente para la rotación:

$\tau = I \alpha\,$

donde:

$\scriptstyle{\tau}$ es el momento aplicado al cuerpo.
$\scriptstyle{I}$ es el momento de inercia del cuerpo con respecto al eje de rotación y
$\textstyle{\alpha={d^2\theta\over dt^2}}$ es la aceleración angular.

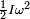La energía cinética de un cuerpo en movimiento con velocidad v es $\scriptstyle{{1\over 2}mv^2}$ , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es $\scriptstyle{{1\over 2}I\omega^2}$ . Donde I es el momento de inercia con respecto al eje de rotación.

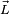La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular $\scriptstyle{\vec L}$ :

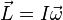
$\vec L = I\vec \omega$

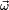El vector momento angular tiene la misma dirección que el vector velocidad angular $\scriptstyle{\vec \omega}$ .

Momentos de inercia de cuerpos simples

Momentos de inercia de algunos sólidos. En el caso de esferas o cilindros llenos, el radio interno vale cero. M es la masa del sólido.

Momentos de inercia de cuerpos simples
Descripción		$I$
varilla respecto a un eje que pasa por su centro		$\frac {mr^2} {12}$
anillo delgado respecto al eje		$mr^2 \,$
anillo delgado respecto a un diámetro		$\frac {mr^2}{2}$
cilindro macizo respecto a su eje de revolución		$\frac {mr^2}{2}$
esfera respecto a un diámetro		$\frac {2mr^2}{5}$

Teorema de ejes paralelos

El teorema de Steiner o de ejes paralelos permite, conocidos los momentos respecto a ejes que pasen por el centro de gravedad, calcular muy fácilmente los momentos de inercia respecto a ejes paralelos que no pasen por el centro de gravedad. Este "traslado" del segundo momento de inercia, se hace mediante la fórmula:

$I_{eje} = I_{eje}^{(CM)} + Ad_{eje}^2 \,$

Donde:

I_eje - Segundo momento de inercia respecto al eje que no pasa por el centro de masa.
I^(CM)_eje - Segundo momento de inercia para el eje que pasa por el centro de gravedad.
A - Área de la sección transversal.
d - Distancia entre el nuevo eje y el eje que pasa por el centro de gravedad.