Movimiento circular uniforme
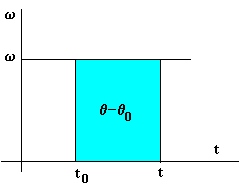 | Un movimiento circular uniforme es aquél cuya velocidad angular w es constante, por tanto, la aceleración angular es cero. La posición angular q del móvil en el instante t lo podemos calcular integrandoq -q0=w(t-t0)o gráficamente, en la representación de w en función de t. |
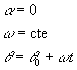
Movimiento circular uniformemente acelerado
 | Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante.Dada la aceleración angular podemos obtener el cambio de velocidad angular w -w0 entre los instantes t0 y t, mediante integración, o gráficamente. |
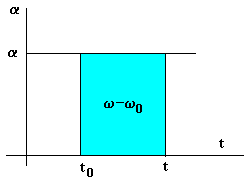
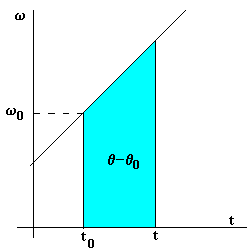 | Dada la velocidad angular w en función del tiempo, obtenemos el desplazamiento q -q0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando |
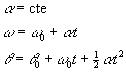
Despejando el tiempo t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ0
Velocidad angular y velocidad tangencial
Velocidad angular es la variación del arco respecto al tiempo, se lo señala con la letra  , se define como:
, se define como:
 , se define como:
, se define como:Velocidad tangencial de la partícula es la velocidad real del objeto que efectúa el movimiento circular, puede calcularse a partir de la velocidad angular. Si vtes la velocidad tangencial, a lo largo de la circunferencia de radio R, se tiene que:
.
Aceleración angular
Se define la aceleración angular como la variación de la velocidad angular por unidad de tiempo y se la representa con la letra:  y se la calcula:
y se la calcula:
 y se la calcula:
y se la calcula:Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Su fórmula principal es:
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo, usualmente segundos. Se mide en hercios o s-1
Aceleración y fuerza centrípetas
La aceleración centrípeta o aceleración normal afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. La fórmula para hallarla es:
La fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la masa del móvil, y basándose en la segunda ley de Newton (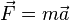 ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:
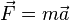 ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:Definición de momento de inercia
El momento de inercia o inercia rotacional es una magnitud que da cuenta de cómo es la distribución de masas de un cuerpo o un sistema de partículas alrededor de uno de sus puntos. Este concepto, desempeña en el movimiento de rotación un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme.
Dado un eje arbitrario, para un sistema de partículas se define como la suma de los productos entre las masas de las partículas que componen un sistema, y el cuadrado de la distancia r de cada partícula a al eje escogido. Representa la inercia de un cuerpo a rotar. Matemáticamente se expresa como:
Para un cuerpo de masa continua (Medio continuo) lo anterior se generaliza como:
El subíndice V de la integral indica que hay que integrar sobre todo el volumen del cuerpo.
Este concepto, desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. Así, por ejemplo, la segunda ley de Newton:  tiene como equivalente para la rotación:
tiene como equivalente para la rotación:
 tiene como equivalente para la rotación:
tiene como equivalente para la rotación:donde:
 es el momento aplicado al cuerpo.
es el momento aplicado al cuerpo. es el momento de inercia del cuerpo con respecto al eje de rotación y
es el momento de inercia del cuerpo con respecto al eje de rotación y es la aceleración angular.
es la aceleración angular.
La energía cinética de un cuerpo en movimiento con velocidad v es  , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es
, mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es 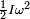 . Donde I es el momento de inercia con respecto al eje de rotación.
. Donde I es el momento de inercia con respecto al eje de rotación.
 , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es
, mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es 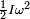 . Donde I es el momento de inercia con respecto al eje de rotación.
. Donde I es el momento de inercia con respecto al eje de rotación.La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular 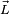 :
:
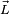 :
:El vector momento angular tiene la misma dirección que el vector velocidad angular 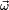 .
.
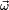 .
.
Momentos de inercia de cuerpos simples
| Descripción | I | |
|---|---|---|
| varilla respecto a un eje que pasa por su centro | 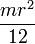 | |
| anillo delgado respecto al eje |  | |
| anillo delgado respecto a un diámetro | 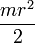 | |
| cilindro macizo respecto a su eje de revolución | 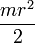 | |
| esfera respecto a un diámetro | 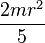 |
Teorema de ejes paralelos
El teorema de Steiner o de ejes paralelos permite, conocidos los momentos respecto a ejes que pasen por el centro de gravedad, calcular muy fácilmente los momentos de inercia respecto a ejes paralelos que no pasen por el centro de gravedad. Este "traslado" del segundo momento de inercia, se hace mediante la fórmula:
Donde:
- Ieje - Segundo momento de inercia respecto al eje que no pasa por el centro de masa.
- I(CM)eje - Segundo momento de inercia para el eje que pasa por el centro de gravedad.
- A - Área de la sección transversal.
- d - Distancia entre el nuevo eje y el eje que pasa por el centro de gravedad.

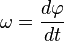
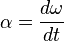




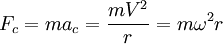
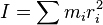


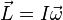


No hay comentarios:
Publicar un comentario